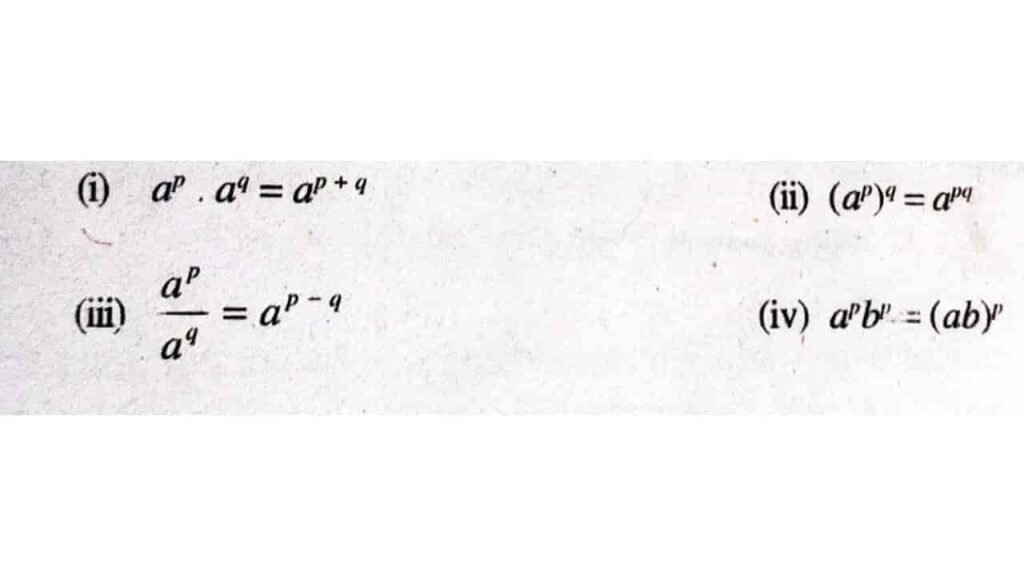Number System Notes Class 9 Maths Introduction
In this chapter you are going to learn about the number system notes class 9 which is about to represent the different types of numbers in the number line.
For example, just imagine that we going in a straight line like a number line and On that number line, you are going in positive numbers. As far we are also seeing there is the only number that nothing.
Since we can conclude that there are many or infinite numbers in Mathematics.
Natural Number
If we collect some number line on that and that collection of numbers denoted
as capital N and not small letter (n) In Addition, collections of numbers after the 0 known Natural Number.
Whole Number
Now we can turn back and we can add zero on that Now we have collected the whole number because when we add 0 to that natural number we get Whole Numbers. Which denoted as W and not the small letter (w).
Integers Number System Notes Class 9 Maths
Moreover, if add some negative numbers on it we will get Integers. The collection of all integers denoted as Z and not small letter (z). This Z denoted because Z came from German word which means Zahlen which means (To Count).
Rational Number
The left numbers are 1/2, 3/4, and -38887/54666 we can also add these numbers and to the collected numbers. Since these collected numbers known as Rational Numbers.
This collection known as or denoted as Q which means Quotient.
Definition of Rational Number class 9
A number can be represented as p/q form where Q is not equal to zero.
Here R is represented as a Rational number.
Rational Numbers.
The left numbers are 1/2, 3/4, and -38887/54666 we can also add these numbers to the collected numbers. Now, these collected numbers known as Rational Numbers.
This collection known as or denoted as Q which means Quotient.
Definition of Rational Number.
A number can be represent as p/q form where Q not equal to zero.
Here R represented as a Rational number.
Irrational Number.
A Number d called irrational and cannot be represented in the form of p/q known as Irrational numbers.
For example. Root 2,3,4,.10110111011110111110…… known as irrational numbers.
Real Number.
A collection of all these types of numbers known as Real numbers. A real number can be denoted as
Summary
- The decimal expansion of an irrational number is non-recurring or recurring in another way we can able to say that terminating or non-terminating.
- All rational or irrational number known as Real numbers.
- There is separate real number corresponding to every point in the number line also the corresponding to each real number there is a separate point in the number line.
- For positive real number a and b the idendity hold is
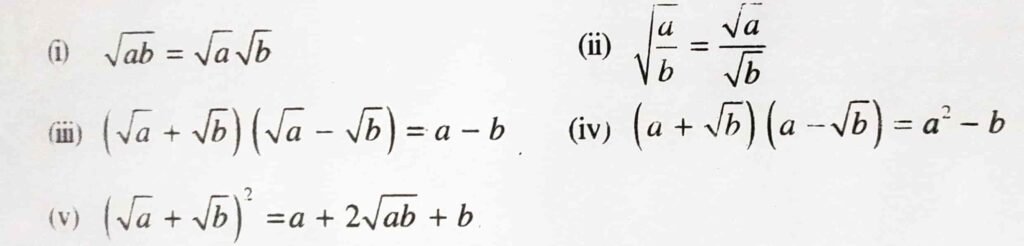
5. Now a 0 be a real number and p and q be a rational number. now the formula will be